The aim of this course is to give an introduction to complex algebraic curves and their study from an algebraic, a topological and a complex-analytical point of view.
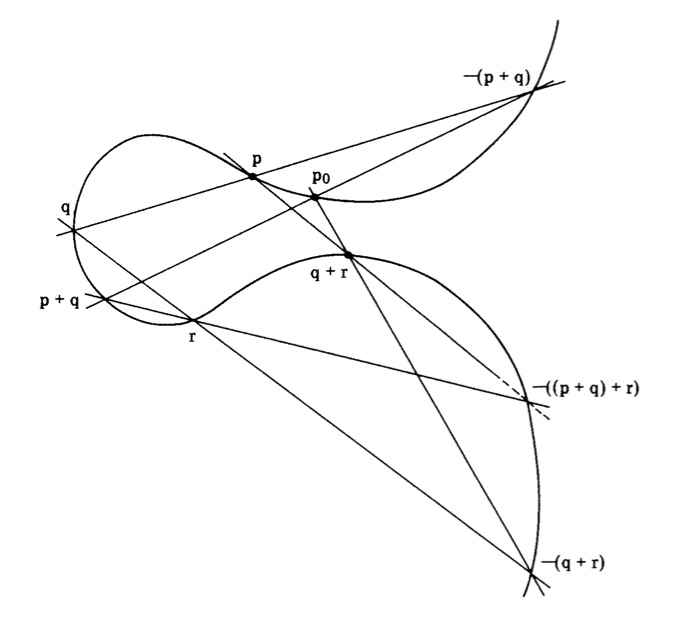
Particular topics of the lecture include: affine and projective complex algebraic curves, intersection multiplicities, Bézout's theorem, Riemann surfaces, the degree-genus formula, the Weierstrass ℘-function, holomorphic differentials, the Riemann-Roch theorem, and curve singularities. Along the way, we will repeatedly encounter elliptic curves and show in multiple ways that their points satisfy a natural group structure. The image for this course is taken from Kirwan's book and illustrates the associativity of this group structure.
- Docente: Livio Liechti
